The transformed equation
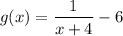 , the graph is shifted 4 units to the left and 6 units down.
, the graph is shifted 4 units to the left and 6 units down.
Step-by-step explanation:
The parent equation is
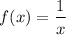
The transformed equation is
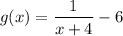
By using the function transformation rules, we can see that the parent function
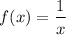 is transformed into the function
is transformed into the function
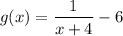
Since, from the function transformation rules, we know that,
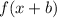 shifts the function b units to the left.
shifts the function b units to the left.
Thus, the transformed function is shifted 4 units to the left.
Also, from the function transformation rules, we know that,
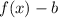 shifts the function b units downward.
shifts the function b units downward.
Thus, the transformed function is shifted 6 units down.
Thus, the transformed equation
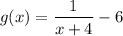 , the graph is shifted 4 units to the left and 6 units down.
, the graph is shifted 4 units to the left and 6 units down.