Answer:
7 units
Explanation:
(Background info, skip if not interested or needed for you)
The equation for distance on a cartesian plane coordinate system is based off the pythagorean theorem.
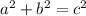
a and b being sides of a right triangle, c being the hypotenuse.
When we are solving for distance we are solving for c essentially.
 =
=
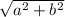
Because a and b are side lengths of the right triangle, we need to find a way to find that in terms of coordinates. So here we might say that a is equal to the horizontal distance between the 2 points or Δx, and we would say that b is the vertical distance between the 2 points Δy.
(solutions)
So essentially distance is:

Now we just use the values given to us, and sub in the x and y values respectively.
(-2,4)
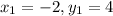
(5,4)
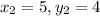
plug these values in:
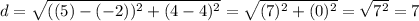
Therefore the distance is 7 units.