Question

nancy and liz are working on a take-home test. normally liz finishes a take-home test in 2 hours less time than nancy. nancy works by herself for 3 hours when liz comes along. together, they finish the job in 2 more hours. how many hours does it take nancy to finish the test on her own?

Answer 1

Nancy can finish the test on her own in 10 hours.

Explanation:

Let the time in which Nancy finish the test on her own be 'x' hours

Now Given:

normally Liz finishes a take-home test in 2 hours less time than Nancy.

Number of hours taken by Nancy =
`x-2\ hours`

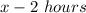
Rate at which Nancy can finish 1 test =
`(1)/(x)\ test/hrs`

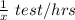
Rate at which Liz can finish 1 test =
`(1)/(x-2)\ test/hrs`

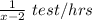
Also Given:

Nancy works by herself for 3 hours when Liz comes along. together, they finish the job in 2 more hours.

so we can say that;

`3((1)/(x))+2(\frac1x+(1)/(x-2))=1\\\\\frac3x+\frac2x+(2)/(x-2)=1\\\\(3+2)/(x)+(2)/(x-2)=1\\\\\frac5x+(2)/(x-2)=1`

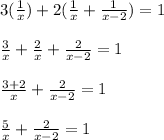
Now We will make the denominator common using LCM we get.

`(5(x-2))/(x(x-2))+(2x)/(x(x-2))=1\\\\(5x-10)/(x(x-2))+(2x)/(x(x-2))=1`

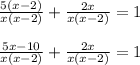
Now Denominator are common so we will solve the Numerator we get;

`(5x-10+2x)/(x(x-2))=1\\\\(7x-10)/(x(x-2))=1`

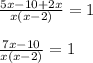
Multiplying both side by
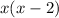`x(x-2)` we get;

`(7x-10)/(x(x-2))* x(x-2) =1* x(x-2)\\\\7x-10=x^2-2x\\\\x^2-2x-7x+10=0\\\\x^2-9x+10=0`

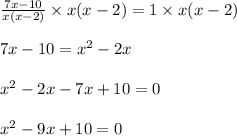
On Factorizing the above equation we will find the roots for x we get;

`x^2+x-10x+10=0\\\\x(x+1)-10(x+1)=0\\\\(x+1)(x-10)=0`

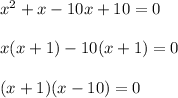
Now we will solve each separately to find the value of 'x' we get;

`x+1=0\\\\x=-1\\\\Or\\\\x-10=0\\\\x=10`

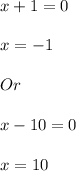
Now we got 2 values for 'x' one positive and one negative.

Since time cannot be negative hence we will consider positive value of x.

Hence Nancy can finish the test on her own in 10 hours.