Answer:
a) There is an 81.87% probability that the instrument does not fail in an 8-hour shift.
b) There is a 45.12% probability of at least one failure in a 24-hour day.
Explanation:
In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

In which
x is the number of sucesses
e = 2.71828 is the Euler number
 is the mean in the given time interval.
is the mean in the given time interval.
a. What is the probability that the instrument does not fail in an 8-hour shift?
The mean for an hour is 0.025 failures.
For 8 hours, we have
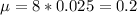
This probability is P(X = 0).

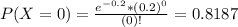
There is an 81.87% probability that the instrument does not fail in an 8-hour shift.
b. What is the probability of at least one failure in a 24-hour day?
The mean for an hour is 0.025 failures.
For 24 hours, we have
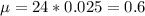
Either we have at least one failure, or we have no failures. The sum of the probabilities of these events is decimal 1. So
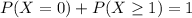
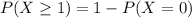
In which

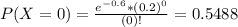
So
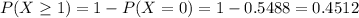
There is a 45.12% probability of at least one failure in a 24-hour day.