Question

Is ABC~ DEF? If so, identify the similarity postulate or theorem that applies.

Answer 1

a

Explanation:

i hope it helps

*correct me if im wrong

Answer 2

The correct answer is:

A. Similar - AA

To determine if triangles
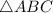`\( \triangle ABC \)`and triangle DEF are similar and identify the similarity postulate or theorem that applies, we need to look at the given angles and side lengths.

The similarity postulates and theorems are:

1. AA (Angle-Angle): If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar.

2. SSS (Side-Side-Side): If the corresponding side lengths of two triangles are proportional, then the triangles are similar.

3. SAS (Side-Angle-Side): If two sides of one triangle are proportional to two sides of another triangle, and the included angles are congruent, then the triangles are similar.

From the image provided:

- Angle B of
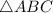`\( \triangle ABC \)`is 105°, and angle E of triangle DEF is also 105°.

- Angle C of triangle ABC is 105°, and angle F of triangle DEF is also 105°.

- The side lengths are given as 16 for triangle ABC and 9 for triangle DEF

Since two angles of triangle ABC are congruent to two angles of triangle DEF (Angle B is congruent to Angle E, and Angle C is congruent to Angle F), the triangles are similar by the AA similarity postulate.