Question

Determine the values of k such that the system of linear equations does not have a unique solution. (Enter your answers as a comma-separated list.)x + y + kz = 9x + ky + z = 2kx + y + z = 5

Answer 1

`\begin{cases}x+y+kz=9\\x+ky+z=2\\kx+y+z=5\end{cases}`

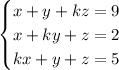
Consider the system in matrix form, with coefficient matrix

`A=\begin{bmatrix}1&1&k\\1&k&1\\k&1&1\end{bmatrix}`

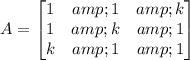
Then the system

`A\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}9\\2\\5\end{bmatrix}`

has a unique solution if
`A` is invertible, which requires that
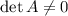`\det A\\eq0`. Compute the determinant: expanding along the first row gives

`\det A=\begin{vmatrix}k&1\\1&1\end{vmatrix}-\begin{vmatrix}1&1\\k&1\end{vmatrix}+k\begin{vmatrix}1&k\\k&1\end{vmatrix}`

`\det A=(k-1)-(1-k)+(1-k^2)=-1+2k-k^2=-(1-k)^2`

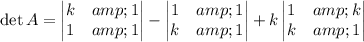
This is zero if
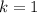`k=1`, and non-zero otherwise, hence there is no unique solution if
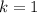`k=1`.