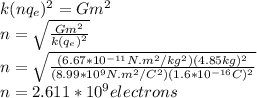Answer:

Step-by-step explanation:
Given data
mass of copper m=4.85 kg
charge of electron qe= -1.6×10⁻¹⁹C
To find
Number of electron n must be removed
Solution
Equate the magnitude of electric force Fe of repulsion between two two spheres to the magnitude of gravitational force of attraction between them
So
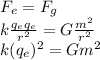
where q is charge of each sphere which is equal to number n of removed electrons multiplied by each charge qe
So