Question

Reagan had $122 in savings account. He deposited $70 each week from his job for the first 5 weeks of summer. In the sixth week, Reagan got a raise and increased his weekly deposits by $12.​

Answer 1

Reagan had $122 in his savings account and deposited $70 each week for 5 weeks. In the sixth week, he increased his deposit by $12. After the sixth week, Reagan had $554 in his savings account.

Step-by-step explanation:

To find out how much Reagan had in his savings account after the sixth week, we need to calculate the total amount he deposited during those weeks. For the first 5 weeks, he deposited $70 each week, so the total amount is 5 * 70 = $<<5*70=350>>350. In the sixth week, he increased his deposit by $12, so the amount for that week is $70 + $12 = $<<70+12=82>>82. Adding the total amount deposited from the first 5 weeks to the amount deposited in the sixth week, we get $350 + $82 = $<<350+82=432>>432. Therefore, Reagan had $122 + $432 = $<<122+432=554>>554 in his savings account after the sixth week.

Answer 2

a. f(x) = (122+70x, 0≤x≤5; 62+82x, x>5}

b. f(8) = 718

c. the amount added in 8 weeks

Step-by-step explanation:

a. Reagan's initial balance is 122. He adds 70 per week, so in terms of x weeks, his balance is ...

f(x) = 122 +70x . . . . . for 0 ≤ x ≤ 5

At 5 weeks, his balance is 122 +70·5 = 472. At that point, he adds 70+12 = 82 per week, so the balance will be ...

f(x) = 472 +82(x -5) = 62 +82x . . . . . for x > 5

So, the piecewise function can be defined as ...

`\displaystyle f(x)=\left\{\begin{array}{ll}122+70x&\text{for $0\le x\le 5$}\\62+82x&\text{for $5<x$}\end{array}\right.`

__

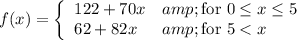
b. f(8) = 62 +82(8) = 718

__

c. f(8) - 122 is the balance after 8 weeks less the initial balance, so represents the amount added to the account in 8 weeks.