Question

At a gas station, 40% of the customers use regular gas (A1), 35% use mid-grade gas (A2), and 25% use premium gas (A3). Of those customers using regular gas, only 30% fill their tanks (event B). Of those customers using mid-grade gas, 60% fill their tanks, whereas of those using premium, 50% fill their tanks.

a. What is the probability that the next customer will requestplus gas and fill their tank ?
b. What is the probability that the next customer fills the tank ?
c. If the next customer fills the tank, what is the probability that the regular gas is requested?

Answer 1

(a) 0.12

(b) 0.455

(c) 0.264

Explanation:

We are given that Probability of customers using regular gas,P(A1) = 0.4

Probability of customers using mid-grade gas,P(A2) = 0.35

Probability of customers using premium gas,P(A3) = 0.25

Let Event B = Customers fill their tank

So, P(B/A1) = 0.3 {This means that Probability that customers fill their tank given they are using regular gas is 30%}

Similarly P(B/A2) = 0.6 and P(B/A3) = 0.5

Now, In general P(A/B) =
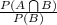`(P(A\bigcap B))/(P(B))` or
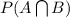`P(A\bigcap B)` = P(A/B) * P(B) .

(a) Probability that the next customer will request regular gas and fill their tank =
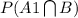`P(A1\bigcap B)` {For happening of both events we use intersection sign}

= P(B/A1) * P(A1) [Note:
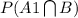`P(A1\bigcap B)` is same as
`P(B\bigcap A1)` )

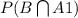= 0.3 * 0.4 = 0.12

(b) Probability that the next customer fills the tank is given by the cases:

• Customer uses regular gas and fills the tank -
  `P(A3\bigcap B)`

• Customer uses mid-grade gas and fills the tank -
  `P(A2\bigcap B)`

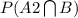
• Customer uses regular gas and fills the tank -
  `P(A1\bigcap B)`

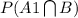
So, P(B) =
`P(A1\bigcap B)` +
`P(A2\bigcap B)` +
`P(A3\bigcap B)`

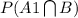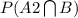= P(B/A1) * P(A1) + P(B/A2) * P(A2) + P(B/A3) * P(A3)

= 0.3 * 0.4 + 0.6 * 0.35 + 0.5 * 0.25 = 0.455

(c) If the next customer fills the tank, probability that the regular gas is requested is given by the expression P(A1/B) because this states the Probability of requesting regular gas given customer has filled the tank.

So, P(A1/B) =
`(P(A1\bigcap B))/(P(B))` =
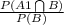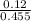`(0.12)/(0.455)` = 0.264