Question

Suppose an electrical wire is replaced with one having every linear dimension doubled (i.e., the length and radius have twice their original values). How is the resistance of the wire affected?

Answer 1

The new resistance becomes half of the initial resistance.

Step-by-step explanation:

The resistance of a wire is given by :

`R=(\rho L)/(A)`

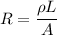
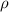`\rho` = resistivity of material

L and A are linear dimension

If the electrical wire is replaced with one having every linear dimension doubled i.e. l' = 2l and r' = 2r

New resistance of wire is given by :

`R'=(\rho L')/(A')`

`R'=(\rho (2L))/(\pi (2r)^2)`

`R'=(1)/(2)(\rho L)/(A)`

`R'=(1)/(2)R`

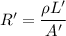
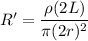
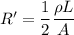
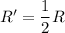
The new resistance becomes half of the initial resistance. Hence, this is the required solution.