Question

In 2003, the Federal Aviation Administration told airlines to assume the average weight of summer passengers (including clothing and carry-on bags) is 190 pounds, with a standard deviation of 35 pounds. Because the population includes male and female adults as well as children, the weights are not normally distributed, but they are nearly normal. A commuter plane carries 24 passengers. What is the probability that the total weight of the passengers exceeds 5000 pounds (the safe flying weight for the aircraft)?

Answer 1

Probability that the total weight of the passengers exceeds 5000 pounds is less than 0.0005%

Explanation:

Given the average weight of summer passengers,
`\mu` = 190 pounds

and standard deviation,
`\sigma` = 35 pounds

Since the weights are nearly following normal so,

Z =
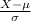`(X - \mu)/(\sigma)` follows standard normal distribution

Let X represents total weight of the passengers.

So Probability(X>5000) = P(
`(X - \mu)/(\sigma)` >
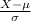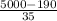`(5000-190)/(35)`) = P(Z > 137.43)

Since we will not be able to calculate this probability using Z table as the highest value in Z % table is given by 4.4172 which is way less than 137.43 so we can only say that this probability will be less than 0.0005% .