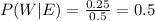Answer:
Explanation:
For this case we define the sampling space :
S= {1,2,3,4,5,6,7,8,9,10,11,12}
And then we define the following events:
E= the roll is even. And the outcomes for E are {2,4,6,8,10,12}
W= roll is greater than or equal to 7. And the outcomes for W are {7,8,9,10,11,12}
And we can find the probabilities for the two events like this:
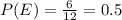
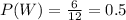
If you were to roll the die and someone tells you that the result was even, what is the probability that the roll isgreater than or equal to 7?
For this case we want a conditional probability given by:
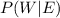
And using the bayes theorem we have this:

The intersection between E and W are the elements {8,10,12}
And then the probability

And then we can find the probability desired like this: