Answer:
As Per Provided Information
An ellipse has a vertex at (0, −7), a co-vertex at (4, 0), and a center at the origin (0,0) .
We have been asked to find the equation of the ellipse in standard form .
As we know the standard equation of an ellipse with centre at the origin (0,0). Since its vertex is on y-axis
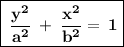
where,
Substituting these values in the above equation and let's solve it
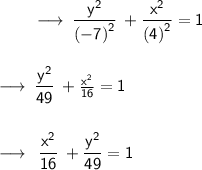
Therefore,
- Required standard equation is x²/16 + y²/16 = 1
So, your answer is 2nd Picture.