Question

If two successive resonant frequencies for an open ended organ pipe (open at both ends) are 801 Hz and 890 Hz, and the speed of sound in air is 343 m/s, determine the following.

(a) frequency of the fundamental Hz
(b) length of the pipe m

Answer 1

Step-by-step explanation:

Given that, two successive resonant frequencies for an open ended organ pipe (open at both ends) are 801 Hz and 890 Hz.

(a) The frequency in case of organ pipe open at both ends is given by :

`f=(nv)/(2L)`

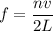
L is the length of the pipe

if f = 801 Hz

`801=(nv)/(2L)`.........(2)

If f = 890 Hz for (n+1)

So,
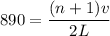`890=((n+1)v)/(2L)`.........(2)

Dividing equation (1) and (2) we get:

`(801)/(890)=(n)/(n+1)`

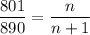
On solving,

n = 9

(b) The speed of sound in air, v = 343 m/s

`f=(nv)/(2L)`

`L=(nv)/(2f)`

`L=(9* 343)/(2* 801)`

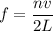
L = 1.92 meters

Hence, this is the required solution.