Question

Starting at 48th Street, Dylan rides his bike due east on Meridian Road with the wind at his back. He rides for 20 minmin at 15 mphmph. He then stops for 5 minmin, turns around, and rides back to 48th Street; because of the headwind, his speed is only 10 mph.How long does his trip take?

Answer 1

To solve this problem we will apply the linear motion kinematic equations. We will start by finding the quantity shifted through the relationship given by the product between speed and time (Time will be converted to hours since the speed is thus specified).

Later, with the given speed we will find the return time.

The general formula of velocity tells us that it is the distance traveled in a certain time, so from it we will obtain the subsequent derivations.

`v = (x)/(t) \Rightarrow x = vt \Rightarrow t = (x)/(v)`

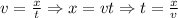
Here,

x = Distance

t = Time

Amount of distance traveled for 20 mins

`x = (15(miles)/(hour))(20 min (1hour)/(60min))`

`x = 5miles`

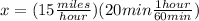
Amount time taken to return back

`t = (x)/(v)`

`t = (5 miles)/(10mph)`

`t = (1)/(2) h = 30minutes`

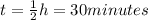
Total time taken

`T = 20+5+30`

`T = 55minutes`

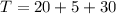
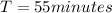
Therefore he takes around of 55 minutes to do that trip.