Question

Examine this system of equations. Which numbers can be multiplied by each equation so that when the two equations are added together, the y term is eliminated? One-fourth x minus one-sixth y = 5 Four-fifths x + StartFraction 3 Over 8 y EndFraction = 10

Answer 1

Answer: A. 18 times the first equation and 8 times the second equation

Explanation:

Answer 2

The first equation must be multiplied by 18 and second equation must be multiplied by 8

Solution:

Given system of equations are:

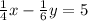`(1)/(4)x -(1)/(6)y = 5` --------- eqn 1

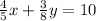`(4)/(5)x +(3)/(8)y = 10` -------------- eqn 2

Multiply the second equation by 8 both sides to remove the fraction in the variable y

`8((4)/(5)x +(3)/(8)y = 10)\\\\(32x)/(5) + 3y = 80 -------- eqn 3`

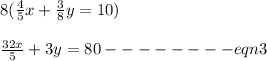
Multiply the first equation by 18 both sides to obtain the coefficient -3 in the variable y

`18((1)/(4)x -(1)/(6)y = 5)\\\\(18)/(4)x -3y = 90 ---------- eqn 4`

Add eqn 3 and eqn 4

`(32)/(5)x +3y +(18)/(4)x -3y = 80+90\\\\(32)/(5)x+(18)/(4)x = 170`

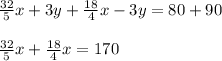
Thus the y-term is eliminated

Therefore, first equation must be multiplied by 18 and second equation must be multiplied by 8