Question

The height of a triangle is 4cm more than twice the length of the base.The area of the triangle is 35 square cm.Find the height of the triangle.​

Answer 1

14cm

Explanation:

Algebra is the way!

But seriously, let's model this algebraically.

We know the that the area of a triangle is represented by:

`A = (1)/(2) base*height`

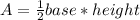
we'll use b and h to represent base and height

`A = (1)/(2) b*h`

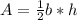
Okay, so you are given the area of the triangle already. It is
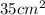`35 cm^2`. SO you have:

`35 = (1)/(2) bh`

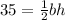
Now here's the tricky bit of the question. You have 2 unknown variables, oh no! How will you solve? The key to this is simple, in a case where you have 2 or more unknown variables, ALWAYS think to yourself, "can I represent this variable in terms of another"?

In this case you can. They tell you what the height of the triangle is, in terms of the length of the base. They tell you, height is 4 cm more than 2 times the base.

So replace h in this equation with 2b + 4.

`35 = (1)/(2) (b)(2b+4)\\\\35 = (1)/(2)(2b^2 + 4b)\\ 70 = 2b^2 + 4b\\0 = 2b^2 + 4b - 70\\0 = (2)(b^2 + 2b - 35)\\0 = (b +7)(b - 5)\\\\b = 5\\b\ \\eq -7`

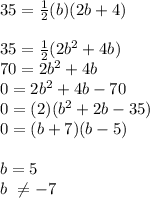
Okay, so you know the base of the triangle is 5 cm. The question asks for height, so what you're going to do is refer back to what h is.

We found that
`h = 2b + 4`

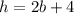
sub in 5 into that:

`h = 2(5) + 4 = 14`

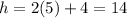
Therefore the height of the triangle is 14cm.

Answer 2

Explanation:

Givens

Area = 1/2 B* H

B = B

H = 2*B + 4

Area = 35

Solution

35 = 1/2 * B * (2B + 4) Multiply both sides by 2

35*2 = 2*(1/2) * B * (2B + 4) Combine

70 = B(2B + 4) Remove the Brackets.

70 = 2B^2 + 4B Subtract 70 from both sides.

2B^2 + 4B - 70 = 0 Divide everything by 2

B^2 + 2B - 35 = 0 Factor

(B + 7)(B - 5)

B+7 = 0 will give a minus number. Geometry does not allow minus numbers.

B - 5 = 0

B = 5

But what you want is the height.

h = 2b + 4

h = 2*5 + 4

Answer: h = 14