Answer:
Explanation:
The given circle has equation
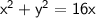
The equation of a circle with center (h,k) and radius r units is
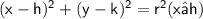
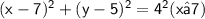
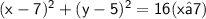
❖ Tip❖ :-
This is the equation that has its center at the origin with radius 4 units.
When this circle is translated seven units to the right and five units up, then the center of the circle will now be at (7,5).