Question

Kayla and Andrea both leave the library at the same time, but in opposite directions. If Andrea travels 5 mph faster than Kayla and after 7 hours they are 119 miles apart, how fast is each traveling?

Answer 1

Kayla: 6 mph

Andrea: 11 mph

Explanation:

Let x represent Kayla's speed.

We have been given that Andrea travels 5 mph faster than Kayla, so Andrea's speed would be
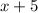`x+5` miles per hour.

We are also told that 7 hours they are 119 miles apart.

`\text{Distance}=\text{Speed}\cdot\text{Time}`

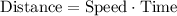
Distance covered by Kayla in 7 hours would be
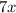`7x` and distance covered by Andrea in 7 hours would be
`7(x+5)`.

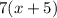Since both are travelling in opposite direction, so we will add both the distances to find total distance as:

`\text{Total distance}=7x+7(x+5)`

`119=7x+7(x+5)`

`119=7x+7x+35`

`119=14x+35`

`119-35=14x+35-35`

`84=14x`

`x=(84)/(14)`

`x=6`

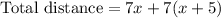
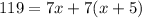
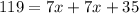
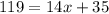
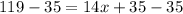
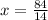
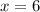
Therefore, Kayla is travelling at a rate of 6 miles per hour.

Andrea's speed would be
`x+5\Rightarrow 6+5=11`

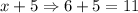
Therefore, Andrea is travelling at a rate of 11 miles per hour.