Question

Two spherical objects are separated by a distance of 2.59 × 10-3 m. The objects are initially electrically neutral and are very small compared to the distance between them. Each object acquires the same negative charge due to the addition of electrons. As a result, each object experiences an electrostatic force that has a magnitude of 4.94 × 10-21 N. How many electrons did it take to produce the charge on one of the objects?

Answer 1

Number of electrons, n = 12 electron

Step-by-step explanation:

Given that,

The distance between charged spheres,
`d=2.59* 10^(-3)\ m`

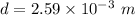
The object experiences an electrostatic force that has a magnitude of,
`F=4.94* 10^(-21)\ N`

The electric force between spheres is given by :

`F=(kq^2)/(d^2)`

`q=\sqrt{(Fd^2)/(k)}`

`q=\sqrt{(4.94* 10^(-21)* (2.59* 10^(-3))^2)/(9* 10^9)}`

`q=1.91* 10^(-18)\ C`

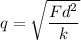
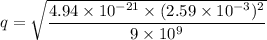
Let there are n number of electrons. Using quantization of electric charge we get :

`q=ne`

`n=(q)/(e)`

`n=(1.91* 10^(-18))/(1.6* 10^(-19))`

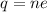
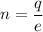
n = 11.93 electrons

or

n = 12 electrons

Hence, 12 electrons produce the charge on one of the objects.