To solve this problem we will apply the concepts related to the Doppler effect. According to this concept, it is understood as the increase or decrease of the frequency of a sound wave when the source that produces it and the person who captures it move away from each other or approach each other. Mathematically this can be described as
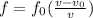
Here,
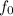 = Original frequency
= Original frequency
 = Velocity of the observer
= Velocity of the observer
 = Velocity of the speed
= Velocity of the speed
Our values are,
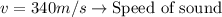
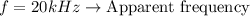
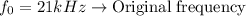
Using the previous equation,
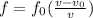
Rearrange to find the velocity of the observer
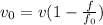
Replacing we have that
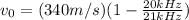
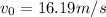
Therefore the velocity of the observer is 16.2m/s