Question

A boat traveled downstream a distance of 45 mi and then came right back. If the speed of the current was 8 mph and the total trip took 3 hourscomma nbspfind the average speed of the boat relative to the water.

Answer 1

Speed of boat is 32 miles per hour that is 4 times speed of water (8 mph).

Explanation:

Let x represent speed of boat in still water.

We have been given that the speed of the current was 8 mph, so the speed of boat downstream would be
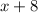`x+8` and speed of boat upstream would be
`x-8`.

`\text{Time}=\frac{\text{Distance}}{\text{Speed}}`

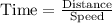
Since boat traveled a distance of 45 miles in 3 hours, so we can set an equation as:

`(45)/(x-8)+(45)/(x+8)=3`

`(45)/(x-8)*(x-8)(x+8)+(45)/(x+8)*(x-8)(x+8)=3(x-8)(x+8)`

`45(x+8)+45(x-8)=3(x-8)(x+8)`

`45x+360+45x-360=3(x^2-64)`

`90x=3x^2-192`

`3x^2-90x-192=0`

`x^2-30x-64=0`

`x^2-32x+2x-64=0`

`x(x-32)+2(x-32)=0`

`(x-32)(x+2)=0`

`(x-32)=0\text{ (or) }(x+2)=0`

`x=32\text{ (or) }x=-2`

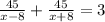
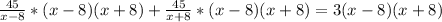
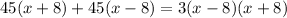
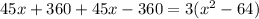
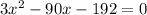
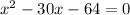
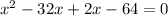
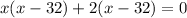
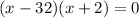
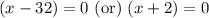
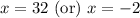
Since speed cannot be negative, therefore, the speed of boat in still water is 32 miles per hour and speed of boat is 4 times speed of water.