Question

The capacity of an elevator is 1515 people or 23852385 pounds. The capacity will be exceeded if 1515 people have weights with a mean greater than 2385 divided by 15 equals 159 pounds.2385/15=159 pounds. Suppose the people have weights that are normally distributed with a mean of 165 lb165 lb and a standard deviation of 30 lb30 lb Find the probability that if a person is randomly​ selected, his weight will be greater than 159159 pounds.

Answer 1

0.57926

Explanation:

We have been given that the capacity of an elevator is 15 people or 2385 pounds. The people have weights that are normally distributed with a mean of 165 lb and a standard deviation of 30 lb. We are asked to find the probability that a randomly selected person has a weight greater than 159 pounds.

First of all, we will find z-score corresponding to 159 using z-score formula.

`z=(x-\mu)/(\sigma)`

`z=(159-165)/(30)`

`z=(-6)/(30)`

`z=-0.2`

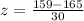
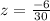
Now, we need to find area under normal distribution curve that is greater than z-score of
`-0.2` as:
`P(z>-0.2)`

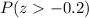
Using formula
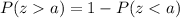`P(z>a)=1-P(z<a)`, we will get:

`P(z>-0.2)=1-P(z<-0.2)`

`P(z>-0.2)=1-0.42074`

`P(z>-0.2)=0.57926`

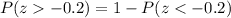
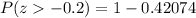
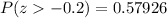
Therefore, the probability that if a person is randomly​ selected, his weight will be greater than 159 pounds, is 0.57926.