Answer:
The numerical limits for a C grade for the test normally distributed are 78 to 80 (rounding the answers to the nearest whole number).
Explanation:
We know how to use the z-scores to consult a standard normal table to find the probabilities associated with those z-scores. However, in this case, we need to go in inverse order, that is, knowing the probabilities associated with obtaining a C, we need to get the z-score associated with it.
We know that the standard normal table is a normal distribution with mean=0 and standard deviation=1 and to find the probabilities for every set of data normally distributed, we use a transformation, that is, the z-scores:
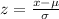
Where x is the value we want to get its probability using the standard normal table,
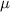 is the population mean and
is the population mean and
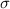 is the population standard deviation. In this case, the population mean is 72.8, and the standard deviation is 9.4.
is the population standard deviation. In this case, the population mean is 72.8, and the standard deviation is 9.4.
According to Academic grading in the United States (2020), in Wikipedia, the "most used grading system" in public high schools indicates that Letter Grade C is between the values of 70% and 79%.
With all this information at hand, we can solve this question as follows:
Finding Lower limit
What is the z-score associated with a probability of 70% (0.70)?
Consulting the cumulative standard normal table, we obtain an approximate value of z = 0.52 for a probability of 0.70 (more precisely, 0.69847).
Then, we need to solve the next equation for x:
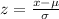
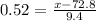
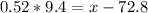
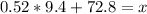
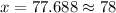 (rounding to the nearest whole number)
(rounding to the nearest whole number)
The lower limit is, as a result, 78.
Finding Upper limit
We apply the same procedure as before:
The z-score associated with a probability of 79%(0.79, or more precisely 0.78814 ) is z = 0.80.
We also need to solve the following equation for x:
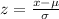
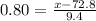
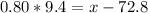
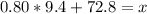
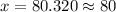
The upper limit is 80.
The area in the Normal Distribution defined by these lower and upper limits can be seen in the graph below.