Answer:
A player can select the five numbers in 38,955,840 ways.
Explanation:
The order is important, for example
The sequence 1-35-32-33-34 is a different sequence than 35-1-32-33-34. Also, the elements cannot be repeated. So we use the permutations formula:
Permutations formula:
The number of possible permutations of x elements from a set of n elements is given by the following formula:
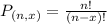
In this problem, we have that:
There are 35 numbers from 1 to 35, so

We are choosing 5 elements, so
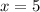
In how many ways can a player select the five numbers?
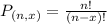
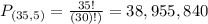
A player can select the five numbers in 38,955,840 ways.