Answer:
The roots of the polynomial equation
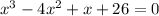 are
are
 .
.
Explanation:
The polynomial provided is:
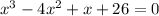
As the polynomials highest degree is 3 there will be 3 roots of the polynomial equation.
The first root can be determined by the hit-and-trial method.
For x = 2,
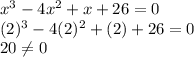
For x = - 2
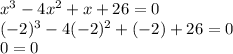
Thus, one of the roots of the polynomial
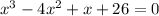 is
is
 or one factor is
or one factor is
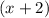 .
.
Now divide he polynomial with this factor as follows:
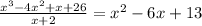
The resultant polynomial is a quadratic equation.
Solve the equation
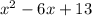 as follows:
as follows:
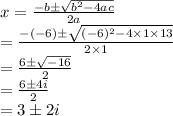
Thus, the roots of the polynomial equation
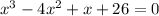 are
are
 .
.