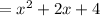Question

X^3-8/x-2
simplify and I need an explanation please

Answer 1

Answer:
`x^2+2x+4`

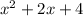
Explanation:

The expression given in the exercise is:

`(x^3-8)/(x-2)`

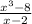
If you descompose the number 8 into its prime factors, you get that:

`8=2*2*2=2^3`

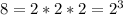
Therefore, you can rewrite the numerator of the expression as following:

`=((x^3-2^3))/((x-2))`

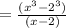
For this exercise you need to remember that for a Difference of cubes:

`a^3-b^3=(a-b)(a^2+ab+b^2)`

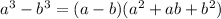
Then, applying this, you get:

`=((x-2)(x^2+2x+2^2))/((x-2))=((x-2)(x^2+2x+4))/((x-2))`

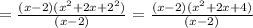
Now, it is necessary to remember the following:

`(a)/(a)=1`

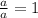
Knowing the above, you can say that:

`((x-2))/((x-2))=1`

Therefore applying this, you get that the simplified expression is:

`=x^2+2x+4`