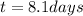Step-by-step walkthrough:
a.
Well a standard half-life equation looks like this.
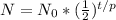
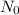 is the starting amount of parent element.
is the starting amount of parent element.
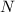 is the end amount of parent element
is the end amount of parent element
 is the time elapsed
is the time elapsed
 is a half-life decay period
is a half-life decay period
We know that the starting amount is 74g, and the period for a half-life is 2.8 days.
Therefore you can create a function based off of the original equation, just sub in the values you already know.
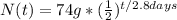
b.
This is easy now that we have already made the function. Here we just reuse it, but plug in 2.8 days.

c.
Now we just gotta do some algebra. Use the original function but this time, replace
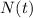 with 10g and solve algebraically.
with 10g and solve algebraically.
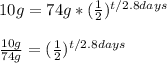
Take the log of both sides.
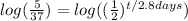
Use the exponent rule for log laws that,
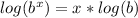
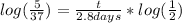
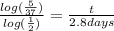

slap that in your calculator and you get