Question

What is the most precise name for a quadrilateral with the following vertices:

A(2,3) B(7,2) C(6,-1) D(1,0)
A) Quadrilateral
B) Parallelogram
C) Rhombus
D) Rectangle

Answer 1

The most precise name for a quadrilateral ABCD is a parallelogram

Explanation:

we have

A(2,3) B(7,2) C(6,-1) D(1,0)

Plot the quadrilateral'

using a graphing tool

The quadrilateral ABCD in the attached figure

Verify the length of the sides

the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

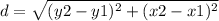
step 1

Find distance AB

A(2,3) B(7,2)

substitute

`d=\sqrt{(2-3)^(2)+(7-2)^(2)}`

`d=\sqrt{(-1)^(2)+(5)^(2)}`

`d_A_B=√(26)\ units`

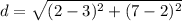
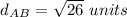
step 2

Find distance BC

B(7,2) C(6,-1)

substitute

`d=\sqrt{(-1-2)^(2)+(6-7)^(2)}`

`d=\sqrt{(-3)^(2)+(-1)^(2)}`

`d_B_C=√(10)\ units`

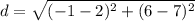
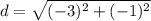
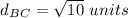
step 3

Find distance CD

C(6,-1) D(1,0)

substitute

`d=\sqrt{(0+1)^(2)+(1-6)^(2)}`

`d=\sqrt{(1)^(2)+(-5)^(2)}`

`d_C_D=√(26)\ units`

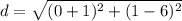
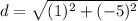
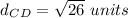
step 4

Find distance AD

A(2,3) D(1,0)

substitute

`d=\sqrt{(0-3)^(2)+(1-2)^(2)}`

`d=\sqrt{(-3)^(2)+(-1)^(2)}`

`d_A_D=√(10)\ units`

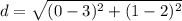
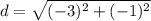
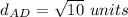
step 5

Compare the length sides

AB=CD

BC=AD

Opposite sides are congruent

Verify the slope of the sides

The formula to calculate the slope between two points is equal to

`m=(y2-y1)/(x2-x1)`

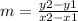
step 1

Find slope AB

A(2,3) B(7,2)

substitute

`m=(2-3)/(7-2)`

`m=(-1)/(5)`

`m_A_B=-(1)/(5)`

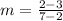
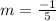
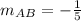
step 2

Find slope BC

B(7,2) C(6,-1)

substitute

`m=(-1-2)/(6-7)`

`m=(-3)/(-1)`

`m_B_C=3`

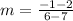
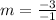
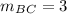
step 3

Find slope CD

C(6,-1) D(1,0)

substitute

`m=(0+1)/(1-6)`

`m=(1)/(-5)`

`m_C_D=-(1)/(5)`

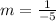
step 4

Find slope AD

A(2,3) D(1,0)

substitute

`m=(0-3)/(1-2)`

`m=(-3)/(-1)`

`m_A_D=3`

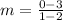
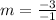
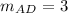
step 5

Compare the slopes

`m_A_B=m_C_D`

`m_B_C=m_A_D`

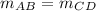
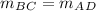
The slope of the opposite sides are equal, that means, opposite sides are parallel

The slopes of consecutive sides are not opposite reciprocal, that means, consecutive sides are not perpendicular

therefore

The most precise name for a quadrilateral ABCD is a parallelogram