Question

A tent has a square floor that measures 9.6 feet on each side. There is a 10-foot zipper in the center of the front panel of the tent that runs from the top of the tent to the floor. The tent has a center pole for support. Find the length of the center pole to the nearest tenth of a foot.

Answer 1

Answer:
`8.8\ ft`

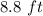
Explanation:

You need to draw a right triangle as the one attached, where "x" is the lenght of the tent's center pole.

For this exercise you can apply the Pythagorean Theorem to solve it. Remember that this is:

`a^2=b^2+c^2`

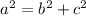
Where "a" is the hypotenuse of the Right triangle and "b" and "c" are the legs of the Right triangle.

If you solve for one of the legs, you get:

`a^2-c^2=b^2\\\\b=√(a^2-c^2)`

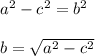
In this case, you can identify that:

`a=10\ ft\\\\b=x\\\\c=4.8\ ft`

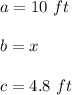
Finally, you must substitute those known values into
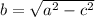`b=√(a^2-c^2)` in order to find the lenght of the center pole.

Therefore, rounded to the nearest tenth of a foot, you get that the value of "x" is the following:

`x=√((10\ ft)^2-(4.8\ ft)^2)\\\\x\approx8.8\ ft`