Answer:
t = 32.3 min
Explanation:
This is an example of half-life exponential decay.
For situations like this we have a formula.
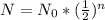
N represents the end amount of parent element, N (naught) represents the starting amount of the parent element, and n being the amount half-lifes that have occurred.
Now n, can be broken down further into t/p, which means the time elapsed (t) divided by time it takes for one decay period (p), which essentially gives you the amount of half-lifes that have occurred. So you can represent the formula as:
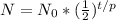
The question tells you you start off with 980 grams of Element x, so put that for N naught.
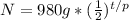 . Then it tells you half-life is 7 minutes, which means the period it takes for one half-life to occur is 7, which is p.
. Then it tells you half-life is 7 minutes, which means the period it takes for one half-life to occur is 7, which is p.
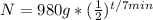 . You are also told that you end up with 40 grams, so put that in for N.
. You are also told that you end up with 40 grams, so put that in for N.
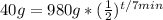 . Now we solve for t, the time elapsed.
. Now we solve for t, the time elapsed.
(This is the part where you use logs to solve, but if you are still rough on this, I'll walk you through it)
Start off by dividing on both sides.
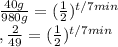
Take the log of both sides.
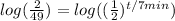
Now we gotta get t out of the exponent, we'll do this by using log laws. More specifically the exponent law for log laws which states.
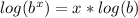 . If we apply that to our situation like so..
. If we apply that to our situation like so..
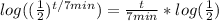
Now our whole equation now looks like this:
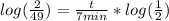
keep simplifying,
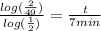
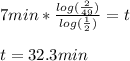
Now you have your answer!