Question

Darla found that the least common denominator needed to subtract \frac{x}{x^2+4x-12}-\frac{3}{x+6}is (x + 6)(x – 2). Which is the correct next step?

\frac{x−3}{x^2+3x−18}
x/(x+6)(x−2) – 3(x−2)/(x+6)(x−2)
x/(x+6)(x−2) – 3(x+6)/(x+6)(x−2)
x(x+6)(x−2)/(x+6)(x−2) – 3(x+6)(x−2)/(x+6)(x−2)

Answer 1

x/((x+6)(x-2)) - 3(x-2)/((x+6)(x-2))

Step-by-step explanation:

Answer 2

Answer: Choice B

`(x)/((x+6)(x-2)) - (3(x-2))/((x+6)(x-2))`

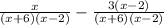
which is the same as x/((x+6)(x-2)) - 3(x-2)/((x+6)(x-2))

=====================================

Step-by-step explanation:

The LCD is (x+6)(x-2) which is the factorization of x^2+4x-12, and that is the denominator of the first fraction. The first fraction has the LCD already. The second fraction does not. It has (x+6) but it is missing (x-2).

We multiply top and bottom of the second fraction by (x-2) to get the second fraction to have the LCD.

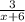`(3)/(x+6)` turns into
`(3)/(x+6)*(x-2)/(x-2) = (3(x-2))/((x+6)(x-2))`

------

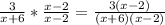
So,

`(x)/(x^2+4x-12) - (3)/(x+6)`

`(x)/((x+6)(x-2)) - (3)/(x+6)`

`(x)/((x+6)(x-2)) - (3(x-2))/((x+6)(x-2))`

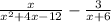
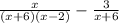
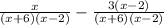
This is the same as x/((x+6)(x-2)) - 3(x-2)/((x+6)(x-2))

Note the parenthesis around "(x+6)(x-2)"

Instead of x/(x+6)(x-2) you should write x/( (x+6)(x-2) ) to ensure that all of "(x+6)(x-2)" is in the denominator.