Question

Geometric Probability

Acellus
Find the probability that a
randomly selected point within the
circle falls in the red shaded area.
r = 4 cm
p = [?]
Enter a decimal rounded to the nearest hundredth.
Enter

Answer 1

The probability is 0.32

Explanation:

we know that

The probability that a randomly selected point within the circle falls in the red shaded area is equal to divide the area of the red shaded area by the area of the circle

step 1

Find the area of the circle

`A=\pi r^(2)`

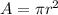
we have

`r=4\ cm\\\pi=3.14`

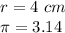
substitute

`A=(3.14)(4)^(2)=50.24\ cm^2`

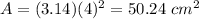
step 2

Find the area of the red shaded area (triangle)

The area of red triangle is

`A=(1)/(2)(b)(h)`

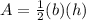
we have

`b=2r=2(4)=8\ cm\\h=r=4\ cm`

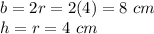
substitute

`A=(1)/(2)(8)(4)=16\ cm^2`

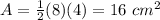
step 3

Find the probability

`(16)/(50.24)= 0.32`