Question

The radius of a krypton atom is 110pm and it's mass is 1.39x10 to -22 g.

What is the density of the atom in grams per cubic centimeter?

Answer 1

`24.9~g/cm^3`

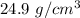
Step-by-step explanation:

Density is found dividing mass by volume. In this case, we treat krypton as a sphere having a volume of
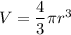`V = (4)/(3)\pi r^3`. Given:

`m = 1.39\cdot 10^(-22)~g`

`r = 110 pm = 1.10\cdot 10^(-8)~cm`

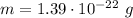
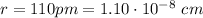
We obtain density of:

`d = (m)/(V) = (m)/((4)/(3)\pi r^3) = (3m)/(4\pi r^3)`

`d = (3\cdot 1.39\cdot 10^(-22)~g)/(4\pi\cdot (1.10\cdot 10^(-8)~cm)^3) = 24.9~g/cm^3`

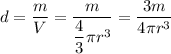
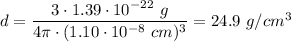
This is not a feasible value for a gas like krypton, its radius is actually not 110 pm.