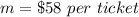Question

When ordering tickets online, a college theater charges a $5 handling fee no matter how large the order. tickets to a comedy concert cost $58 each. If you had to graph the line showing the total cost, y, of buying x tickets, what would the slope of your line be? Explain your thinking.

Answer 1

The slope is
`m=\$58\ per\ ticket`

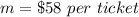
Explanation:

Let

x ---> the number of tickets

y ---> the total cost

we know that

The equation of a line in slope intercept form is equal to

`y=mx+b`

where

m is the slope

b is the y-intercept

In this problem we have that

The slope or unit rate is the cost of one ticket

`m=\$58\ per\ ticket`

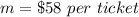
The y-intercept is the same that the handling fee charge

`b=\$5`

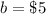
so

The linear equation that represent this situation is

`y=58x+5`

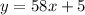
therefore

The slope is
`m=\$58\ per\ ticket`