Answer:
Part A)
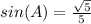
Part B)
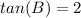
Part C)

Explanation:
see the attached figure to better understand the problem
step 1
Find the length side AB (hypotenuse of the right triangle)
Applying the Pythagorean Theorem
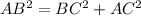
substitute the given values
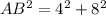
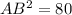

simplify
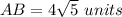
step 2
Find sin(A)
we know that
In the right triangle ABC
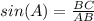 ----> by SOH (opposite side divided by the hypotenuse)
----> by SOH (opposite side divided by the hypotenuse)
substitute the given values
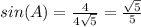
step 3
Find tan(B)
we know that
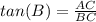 ----> by TOA (opposite side divided by adjacent side)
----> by TOA (opposite side divided by adjacent side)
substitute the values
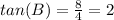
step 4
Find sec(A)
we know that
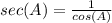
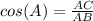 ----> by CAH
----> by CAH
so
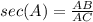
substitute the values
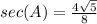
simplify
