Answer:
Assume that the air resistance on this glob of putty is negligible. Let
 .
.
- The velocity of the glob of putty is approximately
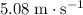 right before it hits the ceiling.
right before it hits the ceiling. - It would take about
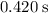 for the glob of putty to reach the ceiling.
for the glob of putty to reach the ceiling.
Step-by-step explanation:
Assume that the air resistance on this glob of putty is negligible. Because of gravity, the glob of putty would accelerate downwards at a constant
 . Since the acceleration points downwards, its value should be negative.
. Since the acceleration points downwards, its value should be negative.
Consider the equation for an object under constant acceleration, where the time taken is unknown.
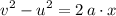 ,
,
where
 is the final velocity of the object. In this case, the value of
is the final velocity of the object. In this case, the value of
 is the initial velocity of the object. In this case,
is the initial velocity of the object. In this case,
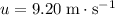 . Note that in this case,
. Note that in this case,
 is the acceleration on the object. In this case,
is the acceleration on the object. In this case,
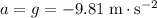 .
.
 is the displacement of the object (during the time when its velocity changed from
is the displacement of the object (during the time when its velocity changed from
 to
to
 .) In this case,
.) In this case,
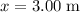 . The value of
. The value of
Rearrange the equation for
 :
:
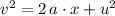 .
.
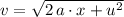 .
.
Calculate the value of
 :
:
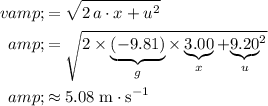 .
.
It is assumed that there's no air resistance on the glob of putty. As a result, the acceleration of the putty would be constant. The duration of this motion can be found with the equation:
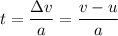 ,
,
where again,
 is the final velocity of the blob of putty,
is the final velocity of the blob of putty,
 is the initial velocity of the blob of putty, and
is the initial velocity of the blob of putty, and
 is the acceleration of the blob of putty.
is the acceleration of the blob of putty.
Based on the previous conclusion,
 . Once again,
. Once again,
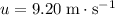 and
and
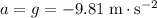 . (Keep in mind that the value of the acceleration of the blob is negative.)
. (Keep in mind that the value of the acceleration of the blob is negative.)
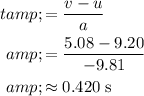 .
.
Note that the inputs
 ,
,
 , and
, and
 here are all in standard units. As a result, the value of
here are all in standard units. As a result, the value of
 and
and
 from the formula would also be in standard units.
from the formula would also be in standard units.