Answer:
Option (a) is correct.
Explanation:
We know that area of the circle is
 where r is the radius of the circle.
where r is the radius of the circle.
Let
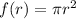
Differentiate with respect to r
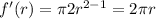
As
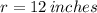 ,
,
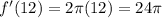
Also, its given that

We know that as per linear approximation to estimate the resulting error,
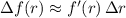
Put

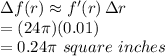
Therefore,
the error is
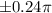
So, option (a) is correct.