Question

A differential equation is given along with the field or problem area in which it arises. Classify it as an ordinary differential equation​ (ODE) or a partial differential equation​ (PDE), give the​ order, and indicate the independent and dependent variables. If the equation is an ordinary differential​ equation, indicate whether the equation is linear or nonlinear.

[y + (dy/dx)²] = C ​,
where C is a constant ​(brachistochrone problem, calculus of​ variations).
Classify the given differential equation. Choose the correct answer below:

A. linear ordinary differential equation
B. nonlinear ordinary differential equation
C. partial differential equation

Answer 1

Option A

Explanation:

Given differential equtaion is
`y+\left ( \frac{\mathrm{d} y}{\mathrm{d} x} \right )^2=C`

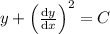
As this equation contains derivatives and not partial derivatives, this equation is an ordinary differential equation and not a partial differential equation.

Here,
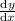`\frac{\mathrm{d} y}{\mathrm{d} x}` denotes that x is an independent variable and y is a dependent variable.

Order of the differential equation is a number of the highest derivative.

Order of the given differential equation is 1.

We can write this ordinary differential equation as follows:

`y+\left ( \frac{\mathrm{d} y}{\mathrm{d} x} \right )^2=C\\\left ( \frac{\mathrm{d} y}{\mathrm{d} x} \right )^2=C-y\\\frac{\mathrm{d} y}{\mathrm{d} x}=√(C-y)`

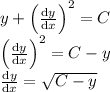
As this equation is of form
`\frac{\mathrm{d} y}{\mathrm{d} x}=f(x,y)`, this is a linear differential equation.

So, option A. is correct as this is a linear ordinary differential equation.