Answer:
a) 4(9
 +2)
+2)
b)6(7
 +1)
+1)
Explanation:
a) Prove that for any positive integer n, 4 evenly divides 32n-1
checking whether the statement is correct or not
∴ n = 1;
=
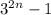
=
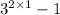
= 9 - 1
= 8
hence it is divisible by 4
Let the statement is for n = k
∴
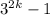 = 4
= 4
 (equation 1)
(equation 1)
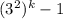 = 4
= 4

 = 4
= 4
 (equation 1)
(equation 1)
Now, we have to proof the statement is true for n = k+1
=
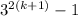
=
 (
(
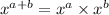 )
)
Adding & Subtracting 8
=
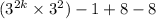
=
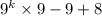
taking common 9
= 9(
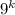 -1)+8
-1)+8
= 9 (4
 ) +8 (from equation 1)
) +8 (from equation 1)
= 36
 + 8
+ 8
= 4(9
 +2)
+2)
if (9
 +2) = p
+2) = p
then = 4p
Since
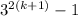 = 4p evenly divisible by 4
= 4p evenly divisible by 4
therefore given statement is true
b)Prove that for any positive integer n, 6 evenly divides

checking whether the statement is correct or not
∴ n = 1;

7 - 1
6
6 is divisible by 6
hence the given statement is true for n = 1
let it also true for n = k
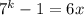 (equation 2)
(equation 2)
Now we have to proof the statement is true for n = k+1
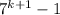
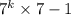
Adding & Subtracting 6
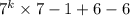
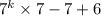
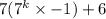
7(6
 )+6 ( from equation 2)
)+6 ( from equation 2)
= 42
 + 6
+ 6
= 6(7
 +1)
+1)
if 6(7
 +1) = p
+1) = p
then = 6p
Since
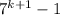 = 6p evenly divisible by 6
= 6p evenly divisible by 6
therefore given statement is true