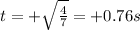Answer:
(a) 0 s
(b) 4.00 m
(c) -0.76 s
(d) +0.76 s
Explanation:
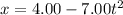
It stops momentarily when the velocity,
 is 0.
is 0.
 is the derivate of
is the derivate of
 .
.
(a)
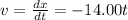
Setting this to 0,
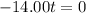
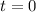
(b) Substitute this value for
 in
in
 to get its position.
to get its position.
 m
m
It passes the origin when


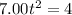
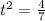
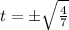
(c) The negative time is
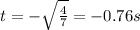
(d) The positive time is