Question

While waiting for the CABS bus on the way home from physics class, your friend looks up at the traffic signal and says, "I wonder how big the traffic signal is, it can't be more than half a meter tall?" Having only a rock, the timer on your phone (no service), your knowledge of kinematics, and all the time in the world, you two decide to figure out its vertical size L.

First you throw the rock vertically upwards so that the maximum height of the rock just matches the height of the bottom of the traffic signal at the peak of the rock’s trajectory. Your friend times that the rock is in the air for a total of tbottom = 2.1 seconds from when you release it to when you catch it (averaging over several trials). Next you throw the rock vertically upwards so that it matches the height at the top of the traffic signal at the peak of its trajectory, and measure it to take ttop = 2.3 seconds (averaging over several trials). What is the approximate vertical size L of the traffic signal?

Answer 1

length of the signal,L is 1.08 m

Step-by-step explanation:

Time of flight in the first case = 2.1 sec

If
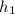`h_(1)` be the maximum height and u be the initial velocity of throw, and

time of ascent = time of descent = ( 2.1/2 ) sec

We get,

v = u - gt

0 = u - 9.8 x (2.1/2)

u = 9.8 x (2.1/2)

= 10.29 m/sec

Now from,

`v^(2) = u^(2)- 2gh_(1)`

`0 = u^(2)- 2gh_(1)`

`h_(1) = (u^(2))/(2g)`

`h_(1) = ((10.29)^(2))/(2* 9.8)`

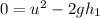
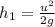
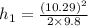
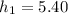`h_(1) = 5.40` m

Similarly, for second throw,

v = u - gt

0 = u - 9.8 x (2.3/2)

u = 11.27 m/sec

Now from,

`v^(2)= u^(2)-2gh_(2)`

`0= u^(2)-2gh_(2)`

`h_(2)= (u^(2))/(2g)`

`h_(2)= ((11.27)^(2))/(2* 9.8)`

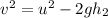
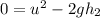
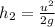
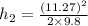
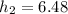`h_(2)= 6.48` m

Length of signal, L =
`h_(2)-h_(1)`

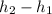
= 6.48 - 5.40

= 1.08 m