Question

A woman sued a computer keyboard manufacturer, charging that her repetitive stress injuries were caused by the keyboard. The injury awarded about $3.5 million for pain and suffering, but the court then set aside that award as being unreasonable compensation. In making this determination, the court identified a "normative" group of 27 similar cases and specified a reasonable award as one within two standard deviations of the mean of the awards in the 27 cases. The 27 awards were (in $1000s):

37, 60, 72, 112, 138, 145, 147, 150, 238, 290, 340, 410, 600, 750, 750, 751, 1050, 1100, 1137, 1150, 1200, 1200, 1250, 1579, 1700, 1825, and 2000.
From which:

Σxᵢ = 20,180 and Σxᵢ² = 23,465,528

What is the maximum possible amount that could be awarded under the two- standard deviation rule?

Answer 1

The maximum possible amount that could be awarded under the two-deviation rule is $ 1.883 Million.

Explanation:

In order to find the maximum possible amount of the award, the formula is given as

`x=\bar{x}+2s`

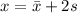
Here

`\bar{x}` is the mean of the samples and is given as

`\bar{x}= (\sum_(i=1)^(n) x_i)/(n)`

s is the standard deviation which is given as

`s=\sqrt{(1)/(n-1) (\sum x_i^2-(1)/(n) (\sum x_i)^2 )}`

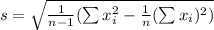
Putting values as

`\sum x_i^2=23,465,528 \$ (1000s) \\ \sum x_i=20,180 \$ (1000s) \\ n=27`

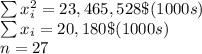
Substituting the values in the equation of mean is as

`\bar{x}= (20,180)/(27) \\ \bar{x}= 747.407 \$ (1000s)`

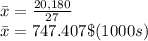
Where as standard deviation is given as

`s=\sqrt{(1)/(27-1) (23,465,528-(1)/(27) (20,180)^2 )} \\ s=\sqrt{(1)/(26) (23,465,528-15082681.4815 )} \\s=\sqrt{(1)/(26) (8382846.51)} \\s=√(322417.17) \\s=567.81 \$ (1000s)`

Putting this in the equation of maximum amount gives

`x=\bar{x}+2.s \\ x=747.407 +2(567.81) \\x=1883.04 \$ (1000s)`

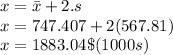
So the maximum possible amount that can be awarded in this case is 1883.04 thousand dollars or $ 1.883 Million. This value is less than the previously maximum value which is $3.5 million.