Answer:
43,680 ways.
Explanation:
We have been given that an experiment involves 16 participants. From these, a group of 4 participants is to be tested under a special condition. We are asked to find the number of groups of 4 participants that can be chosen, assuming that the order in which the participants are chosen is irrelevant.
We will use permutations formula to solve our given problem.

For our given problem
 and
and
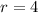 .
.
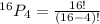
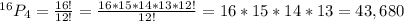
Therefore, 4 participants can be chosen in 43,680 different ways.