Question

Two charges of magnitude q are separated by a distance d. Assuming there are no changes to anything else, but the charges are separated by 3 times their current distance, what will happen to the Coloumb force between them?

Answer 1

The new force between charges becomes (1/9)th of the initial force.

Step-by-step explanation:

The electric force acting between two charges is given by :

`F=(kq_1q_2)/(d^2)`

k is the electrostatic constant

If the two charges are separated by 3 times their current distance, d' = 3d

We need to find the new Coulomb force between the charges. The new force is given by :

`F'=(kq_1q_2)/(d'^2)`

`F'=(kq_1q_2)/((3d)^2)`

`F'=(1)/(9)* (kq_1q_2)/(d^2)`

`F'=(F)/(9)`

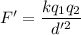
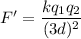
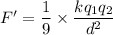
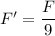
So, the new force between charges becomes (1/9)th of the initial force.