Question

A gas station stores its gasoline in a tank under the ground. the tank is a cylinder lying horizontally on its side. In other words, the tank is not standing vertically on one of its flat ends.

If the radius of the cylinder is 4 feet, its length is 12 feet, and its top is 10 feet under the ground, find the total amount of work needed to pump the gasoline out of the tank. (Gasoline weighs 42 lb/ft³)

Answer 1

W = π*g*(0.365625*p + 0.393375)

Step-by-step explanation:

Solution:

We will take infinitesimal strips of Volume ΔV along the height Δx:

Δ V = pi*r^2 * Height

Δ V = pi*0.5^2 * Δx

Now, we calculate the infinitesimal mass ΔM

ΔM = Density * Volume

ΔM = (1 + p*h)*pi*0.5^2 *Δx

Where, p is measured from water free surface h = x -0.3

ΔM = (1 + (x - 0.3)*p)*pi*0.5^2 *Δx

Force due to gravity is as follows:

ΔF_g = ΔM*g

ΔF_g = (1 + (x - 0.3)*p)*pi*0.5^2 *Δx *g

Work done in moving water distance x:

ΔW = ΔF_g * x

ΔW = (1 + (x - 0.3)*p)*pi*0.5^2 *Δx *g * x

Integrating ΔW over the height b = 0.3 < x < a =0.8 m:

`W = \int\limits^a_b { (1 + (x - 0.3)*p)*pi*0.5^2 *g * x} \, dx \\\\W = pi*0.5^2 *g\int\limits^a_b ({x - 0.3p*x +px^2}) \, dx \\\\W = (pi*g)/(4) (0.5x^2 -0.15p*x +(p*x^3)/(3) )\\\\W = (pi*g)/(4) *(1.62 +1.485p) - (pi*g)/(4) *(0.045 - 0.0045p)\\\\W = pi*g*(0.365625p +0.393375)`

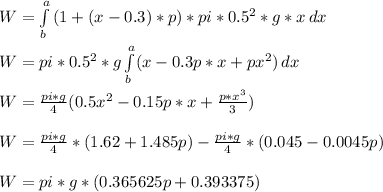
The work done required by the pump is:

W = π*g*(0.365625*p + 0.393375)