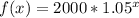Question

Help me!!Write a function using correct notation that models the value of each car.

Answer 1

`f(x) = 2000 * 1.05^x`

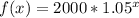
Explanation:

The key to this question is interpreting the graph and then modelling it into an exponential function.

You are given 2 key characteristics of this graph. 1 characteristic being that it intercepts the y-axis at (0,2000), and another characteristic being that it goes through the point (1,2100)

Now refer to the standard form of an exponential function.

`y = a * b^x`

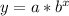
Since you know that when x = 0, y = 2000, a must be 2000. Because
`b^0 = 1`, 2000 * 1 = 2000

So you got your a value. Sub it into the equation and now you got.

`y = 2000 * b^x`

You still need to solve for b, so this is where you do some algebra. Pick your key point, (1,2100), sub in those values for x and y, and solve for b.

`2100 = 2000 * b^1\\(2100)/(2000) = b\\ 1.05 = b`

Now you have your a and b values. Now you can express using a function:

`f(x) = 2000 * 1.05^x`