Question

The table below shows selected points from a function.

Is the statement below True or False?

The rate of change for the interval shown in the table is not constant, so the function is non-linear.

True

False

Answer 1

True

Explanation:

Rate Of Change Of Functions

Given a function y=f(x), the rate of change of f can be computed as the slope of the tangent line in a specific point (by using derivatives), or an approximation by computing the slope of a secant line between two points (a,b) (c,d) that belong to the function. The slope can be calculated with the formula

`\displaystyle m=(d-b)/(c-a)`

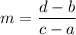
If this value is calculated with any pair of points and it always results in the same, then the function is linear. If they are different, the function is non-linear.

Let's take the first two points from the table (1,1)(2,4)

`\displaystyle m=(4-1)/(2-1)=3`

Now, we use the second and the third point (2,4) (3,9)

`\displaystyle m=(9-4)/(3-2)=5`

This difference in values of the slope is enough to state the function is non-linear

Answer: True