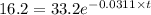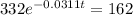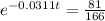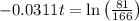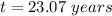Answer:
Step-by-step explanation:
Half life of lead - 210 = 22.3 years

Where, k is rate constant
So,

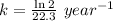
The rate constant, k = 0.0311 year⁻¹
Using integrated rate law for first order kinetics as:
![[A_t]=[A_0]e^(-kt)](https://img.qammunity.org/2021/formulas/chemistry/high-school/p2vpxs9cve2w798wzy926mzqzvfv5si8xr.png)
Where,
![[A_t]](https://img.qammunity.org/2021/formulas/chemistry/high-school/c6se0yk0a5jz0ud2m1a9jh5tv0rk9jx59i.png) is the concentration at time t
is the concentration at time t
![[A_0]](https://img.qammunity.org/2021/formulas/chemistry/high-school/i49y9xugeve1tuhjmf05tpufcmfey5f0yu.png) is the initial concentration
is the initial concentration
Initial concentration
![[A_0]](https://img.qammunity.org/2021/formulas/chemistry/high-school/i49y9xugeve1tuhjmf05tpufcmfey5f0yu.png) = 33.2 mg
= 33.2 mg
Final concentration
![[A_t]](https://img.qammunity.org/2021/formulas/chemistry/high-school/c6se0yk0a5jz0ud2m1a9jh5tv0rk9jx59i.png) = 16.2 mg
= 16.2 mg
Time = ?
Applying in the above equation, we get that:-