Question

If a = 7 × 10−6 C/m4 and b = 1 m, find E at r = 0.6 m. The permittivity of a vacuum is 8.8542 × 10−12 C 2 /N · m2 . Answer in units of N/C

Answer 1

The electric field potential (E) is 1.75 X 10⁵ N/C

Step-by-step explanation:

Electric field potential (E) is force per unit charge.

Electric field potential (E) = force/charge = f/q, unit is Newton (N) per Coulomb (C); N/C

`E = (q)/(4 \pi \epsilon r^2)`

where;

q is charge in coulomb (C)

ε is permittivity of free space = 8.8542 X 10⁻¹² C²/Nm²

`k = (1)/(4 \pi \epsilon) = (1)/(4\pi (8.8542 X 10^(-12))) = 8.99 X10^9 Nm^2/C^2`

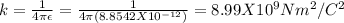
if a = 7 X 10⁻⁶ C/m⁴ and b = 1m

a in "C" =
`7 X 10^-{6} (C)/(m^4) X (1m)^4 = 7 X 10^-{6} C`

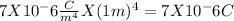
Electric field potential at r = 0.6m =
`(ka)/(r^2)`

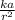
E =
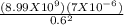`((8.99 X10^9)(7X 10^(-6)))/(0.6^2)` = 1.75 X 10⁵ N/C

Therefore, the electric field potential (E) is 1.75 X 10⁵ N/C